题目再现
P1004 [NOIP 2000 提高组] 方格取数
题目背景
NOIP 2000 提高组 T4
题目描述
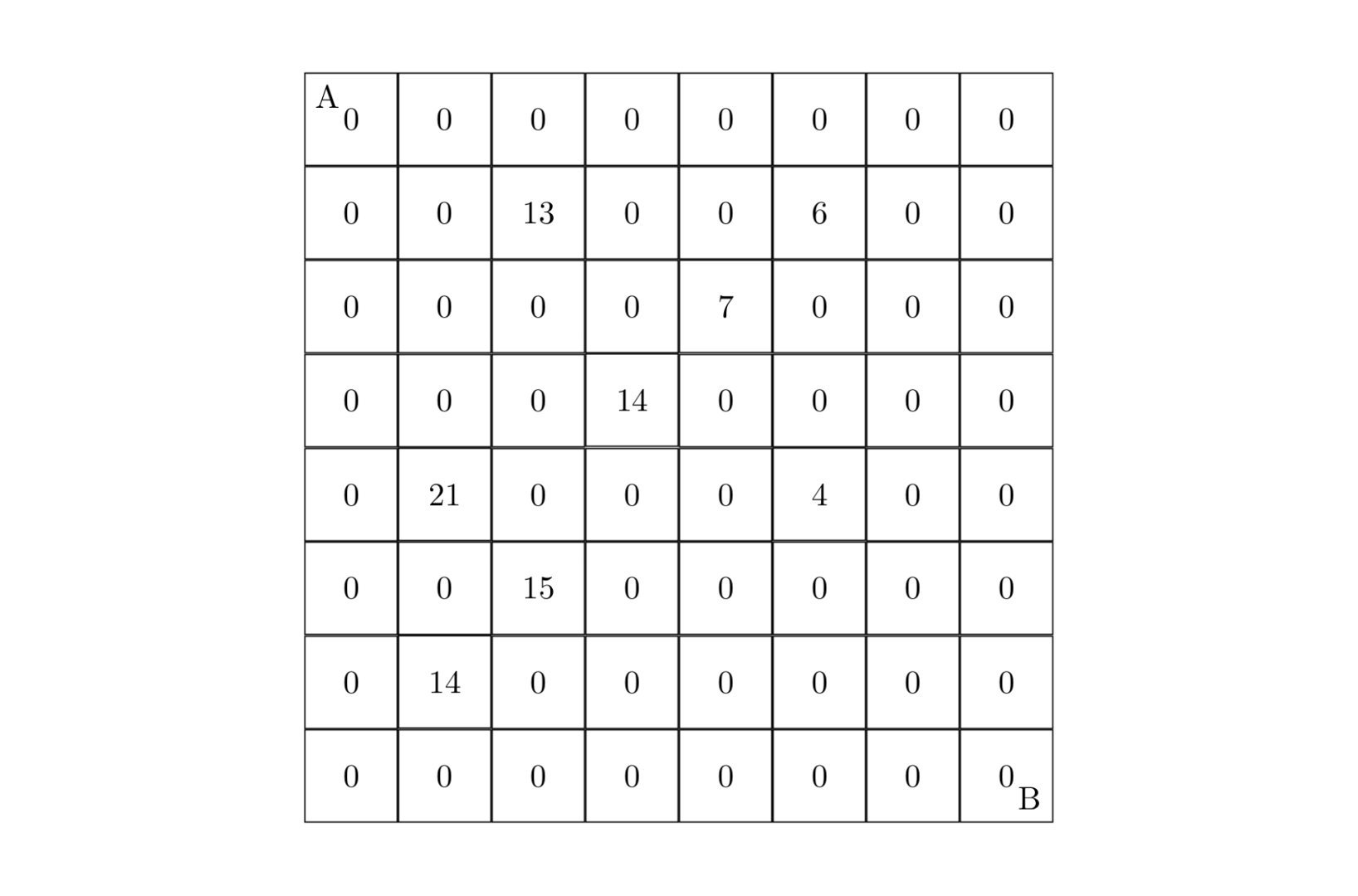
设有 $N \times N$ 的方格图 $(N \le 9)$,我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 $0$。如下图所示(见样例):
某人从图的左上角的 $A$ 点出发,可以向下行走,也可以向右走,直到到达右下角的 $B$ 点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字 $0$)。
此人从 $A$ 点到 $B$ 点共走两次,试找出 $2$ 条这样的路径,使得取得的数之和为最大。输入格式
输入的第一行为一个整数 $N$(表示 $N \times N$ 的方格图),接下来的每行有三个整数,前两个表示位置,第三个数为该位置上所放的数。一行单独的 $0$ 表示输入结束。
输出格式
只需输出一个整数,表示 $2$ 条路径上取得的最大的和。
输入输出样例 #1
输入 #1
8 2 3 13 2 6 6 3 5 7 4 4 14 5 2 21 5 6 4 6 3 15 7 2 14 0 0 0输出 #1
67说明/提示
数据范围:$1\le N\le 9$。
🧠 算法思路简述
- 设计状态
dp[t][x1][x2]表示总共走了 t 步时,第一个人位于 (x1, y1),第二个人位于 (x2, y2),其中 y1 = t - x1,y2 = t - x2。 - 状态转移由四种组合(右右、右下、下右、下下)构成。
- 每步加上当前两个位置的格子值(如果两个点重合只加一次)。
🧭 调试全过程分阶段回顾
阶段 0:初始提交
- 代码状态:safe_max4(t - 1, …) 内部访问的是 dp[t][…]
- 表面现象:样例输出是 29,部分点为乱值
- 根本原因:t = 0 时会访问 dp[-1][…],数组下标越界,触发 undefined behavior(UB)
- 修正措施:加越界保护,如
if (t < 1) return -1;
阶段 1:补越界之后仍错
- 代码状态:加了 t < 1 的保护返回 -1
- 表面现象:样例仍输出 29
- 根本原因:
bool a = (x1 > 0 && t - x1 > 0),误判 y1 = 0 的格子不合法,把第一列所有转移砍掉了 - 修正措施:条件写成
>= 0,或仅保留x1 > 0,其余交由 dp==-1 判定
阶段 2:误判偏移能抵消不等式
- 代码状态:传 safe_max4(t - 1, …),内部又访问 dp[t - 1][…]
- 表面现象:仍然错误
- 根本原因:即使逻辑上你偏移了 t,也无法改变 y=0 时前驱仍为 y=0 的事实,转移仍然被过滤
- 修正措施:明确 y=0 是合法状态,条件必须为
>= 0
阶段 3:最终修正通过所有测试点
- 代码状态:所有转移判断均使用
>= 0,路径判断逻辑完全合理 - 结果:样例 67,自测样例输出 30,全部 AC
🧱 错误要点拆解
1. 越界 ≠ 安全读取
你可能觉得“我只是读一下数组又没写,能有啥事?”但只要下标非法就是 Undefined Behavior,编译器可能直接跳过某个分支甚至整个函数逻辑。
2. 第一行 / 第一列被误判为非法
动态规划中,坐标 (x, y=0) 是完全合法的状态,其前驱 (x, y-1) 有可能不存在,但 (x-1, y) 却是合法的。因此不应把 y=0 直接排除在外。
3. “我偏移了 t,所以 y = 0 不会出现”?错。
即便你在外层传入的是 t - 1,内部再访问 dp[t - 1][...],y = t - x 的表达仍然成立,y=0 的状态仍然会出现,只不过你自己绕了一下写法,逻辑没变。
🎯 最终 AC 代码
#include <bits/stdc++.h>
using namespace std;
const int N = 9;
int mp[N][N], dp[N*2][N][N];
int safe_max4(int t, int x1, int x2) {
if (t < 1) return -1;
bool a = (x1 > 0 && t-x1 >= 0);
bool b = (x2 > 0 && t-x2 >= 0);
return max(
max(a && b ? dp[t-1][x1-1][x2-1] : -1, dp[t-1][x1][x2]),
max(a ? dp[t-1][x1-1][x2] : -1,
b ? dp[t-1][x1][x2-1] : -1)
);
}
int main() {
int n; cin >> n;
int x, y, v;
while (cin >> x >> y >> v, x || y || v) mp[x-1][y-1] = v;
memset(dp, -1, sizeof dp);
dp[0][0][0] = mp[0][0];
for (int t = 0; t <= n*2-2; ++t)
for (int x1 = 0; x1 < n; ++x1)
for (int x2 = 0; x2 < n; ++x2) {
int y1 = t-x1, y2 = t-x2;
if (y1 < 0 || y2 < 0 || y1 >= n || y2 >= n) continue;
int cur = mp[x1][y1];
if (x1 != x2 || y1 != y2)
cur += mp[x2][y2];
int &res = dp[t][x1][x2];
int pre = safe_max4(t, x1, x2);
if (pre >= 0) res = pre + cur;
}
cout << dp[n*2-2][n-1][n-1] << endl;
return 0;
}
✅ 经验建议整理
- 先保证不越界,再谈状态合法性:数组访问不越界是底线,状态转移是否合法可以由 dp 值判断(如 dp==-1)。
- 善用最小极端数据做边界验证:例如 3×3、所有值集中在边角、第一列/行等,能暴露大部分 off-by-one 错误。
- 优先写成
>=再回调测试收紧:对边界的放松更能捕获真实状态,必要时再收紧逻辑。 - 开启编译器或运行时检查工具:如
-fsanitize=address,undefined或使用 Valgrind,可以第一时间发现dp[-1]之类的致命 UB。
🎬 结语
这是一道经典的“不是算法难,是实现难”的动态规划问题。你可能设计了一个很漂亮的状态转移,但只要下标错一个、边界漏一层,最终结果就天差地别。
这道题让我再一次认识到:**写对一个状态转移不难,写对所有边界才是硬功夫。**希望你在看完这篇笔记之后,也能不再被越界和 off-by-one 坑住啦!